テストの採点について。
「5×3≠3×5なのか」
といった話や、
「長方形の面積を求める公式は“たて×よこ”だが、縦5cm・横2cmの長方形を“2×5”で求めてはいけないのか」
といった話など、よくネット上でも話題になりますね。
大抵は、採点基準が数学的真理に反しているケースが話題になるわけですが。
さて、下の答案を見てください。
(4年「垂直・平行と四角形」)
「問題:下の図のような四角形を書きましょう」

線対称。*1
……上の答案を、どうお考えになるでしょうか。
この種の作図問題は、教師用の解答に、確認用の透明シートが付属しています。
シートに赤で図が印刷されており、それを子どもの答案に重ねれば、いちいち角度を測ったりしなくても正しい図かどうか確認できるわけです。
……まあ、上の答案は、試してみるまでもなく重なりませんが。
しかし、裏返したらぴったり重なりました。
6年担任に尋ねてみます。
K村「……裏返して重なる図形って、元の図形と合同なんですよね?」
6担「そうですね」
しかし、「合同」や「線対称」について習うのは6年生。
4年ではまだ習っていません。
6担「これは、わかってて逆向きに書いたんじゃなくて、分度器の使い方を間違っただけかも知れないですよね」
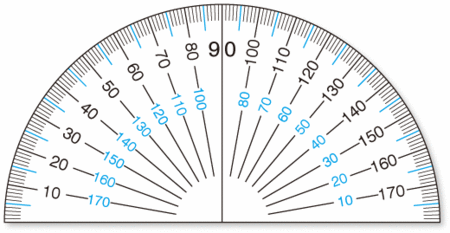
分度器には、左右両方から目盛りがついていますから、100度を作図しようとして80度を書いてしまう、というのは非常に良くあるミスなのです。
「ミスだろうがなんだろうが、合同は合同だろう」
という意見もありましょうが、そもそも、設問は「合同な図形を書け」ではなく「下の図のような四角形を書きましょう」なのです。
「合同」という言葉を習っていないからそういう表現にしたのだ、と考えることもできますが、習っていないのは言葉というより「合同」という概念そのものです。
もちろん、対称移動した図形は合同、というのは、学年と無関係に普遍的な数学的真理です。
しかし、こと、ユークリッド幾何学を離れた日常生活においては、「裏返しても同じ」というのは普遍的真実でもなんでもなく、むしろレアケースです。
「<」と「>」の意味が同じでないように、文字とか設計図とかの鏡像を書いたら許されないわけで。
つまり、この問題は、日常的な意味の「同じ図形」を書かせることを意図したもので、「合同な図形」を書かせることはそもそも意図していない、という可能性もあります。
さて。
結局私がどうしたかというと。
件の答案を書いた子を呼んで、
「君が書いた図は、どこが3cm、4cm、100°なのかね。図の中に書き込むように」
と求めました。
その結果、その子の答えは下のようなものでした。

K村「……よしわかった。じゃあ正解にしとくな」
件の回答を見て、無条件で正答扱いにするよ、という方もいれば、誤答扱いにするよ、という方もいると思います。
そもそも、図そのものは同じなのに、作図の「意図」によって正答か誤答かが分かれるのはおかしい、という意見もあるでしょう。
(図としては同じものを、下のように書いてきた子もいました。
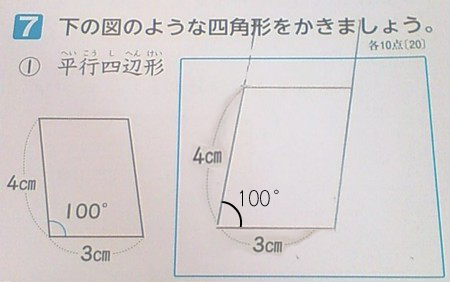
「100°」は提出した時点で記入してあって、これは誤答扱いにしました……)
私としても、これがベストな対応だったという自信はありません。
ただ、人によって正答にすべきかどうか意見が分かれるだろう、という点は、多くの方が理解されると思います。
数学的真理は唯一ですが、それによって、採点基準まで唯一で自明なものに定まるとは限らないのです。
冒頭書いたとおり、ネットで話題になるのは、明らかに採点基準がおかしい場合が多いと思います。
しかしながら、テストの採点においては、もっと微妙で、採点する側も迷うケースが多い、という話でした。
*1:写真で見るとなんだか歪んで見えますが、これは斜め方向から撮影したからです。(長方形である回答欄にもパースがかかっているのがおわかりと思います)
実際には正しく平行四辺形でした。(6年担任にも確認してもらいました)