最初に追記。
この記事は、他所から参考資料としてリンクされてたりするので残してありますが、筆者は、もうこの問題について「順序あり」「順序なし」双方が
「順序がある/ないのは当然だろうそんなことも知らないのか」
的態度を見せるのに辟易しています。
本件について熱心に議論している方は他所にいますので、どうぞ議論はそちらでしていただくようお願いします。
(「貴君と議論をするつもりはない、意見表明をしているだけだ」とのたまった方も過去にいましたが、そういうのはご自分のブログ等でお願いします)
前置き。
先頃はてな界隈で話題になっていた「3×5≠5×3なのか?」の話。

このたった一枚の画像が、擁護しようとする一部学校関係者と、小学生時代のトラウマを刺激された一部はてなーの間で猛烈な論争の種になっていたようです。
はてなー、学校関係者、両方の端くれである私も、久しぶりに小学2年生の指導書を借りて、あれこれ考えたりしていたのですが、考えているうちに時機を逸してしまいました。
まだ考えがまとまらないのですが、とりあえず資料提供。
なにぶん、学習指導要領はネットで確認できますけど、教科書や指導書はそうではないですからね。
*以下、この記事中の画像は、特に断りがない限り、東京書籍の指導書から引用したものです。*1
さて、東京書籍は教科書会社の最大手であり、小学校算数においても最大のシェアを誇っています。*2
2年生のまとめでは。
まず、個人的に一番衝撃だった部分から。
練習問題のページ「力をつけよう」。

(写真が見づらいのは許してください。学校の備品なので、裁断してスキャナにかけるわけにもいきませんでした)
「力をつけよう」というのは、単元の最後の練習問題。
つまり、2年生の九九の学習のまとめです。
「問3」を見てください。

「子どもが6人います。1人にあめを7こずつくばります。
あめは何こいりますか」
余白に、教師向けの「解答」として、赤で
「7×6=42 答え 42こ」
と印刷してありやがりますね?
その欄外。

「問3:問題に出てくる数の通りに式をつくることができない7の段を適用して解く問題」
・6×7と立式する子どもにはあめの図をかかせ、同じ数のまとまりは6なのか7なのかをしっかりとつかませる。
また、6×7では、6人が7つ分になり、答えは子どもの人数となってしまうことをおさえる。
何言ってるのかわからないかも知れませんが……。
要は、東京書籍は「6×7は誤答である」と明言してるわけです。
問3は、「7×6が正しい」という前提のもと、意図的に
「6こずつ7人に配る」
と、数字が文中に出てくる順番を逆にした「ひっかけ問題」という位置づけなのです。
前述の通り、この問題は2年生のかけ算の学習のまとめにあたりますから、少なくとも2年生では、最後まで「5×3≠3×5」というのが、教科書的な理解である……ということになります。
えー……。
納得いかねえ。
正直、私自身の意見は、簡単に言えば(詳しく書いたら長くなった)、
「“5が3つあるときは5×3で計算できるよ”というように教えてやるのは悪くない。
でも、交換法則は正しいんだから、“5×3”と“3×5”、いずれも正解にせざるを得ないんじゃないか」
……という感じです。
学習指導要領にも、“「3×5≠5×3」として指導すべき”……という趣旨の文言はないようなので、教員的にはそこで議論は終わりなんじゃないかな、と思いますが。
それ以上は、極端な話「児童の実態に合わせて指導すべき」という以上のことは言えないわけですから。
なのに、念のため指導書を確認したらこんな記述だったので驚きました。
もちろん、教科書の記述は法令ではありません。
だから、教科書の記述が直ちに学校現場に対し法的拘束力を持つとは言えません。
ただ、これが文科省の検定を経た教科書なのは確かですし、*3学校には検定済み教科書を使う法的義務があるのもまた事実。
(学校教育法第34条)
官僚主義的態度をとるなら、
「教科書にそう書いてあるからこれが正しいのです。
苦情は東京書籍、および検定を担当した文科省にお願いします」
……ということになるでしょうが、教える立場の人間がそこで思考停止することは許されず、教科書会社がどういう意図の元にこういう記述をしているのか、確認しておく必要があるでしょう。
ではなんでこんなことになっているのか。
今度は、かけ算学習の導入まで戻ってみましょう。
はじめてのかけ算。
小学生が、生まれて初めてかけ算を習う時間です。
(まあ、どこかで予習してなければ)

6人乗った車両が3台あるのをどう表すか。
この時点で、2年生は、まだ足し算と引き算しか使えません。
「3台の車に4人、5人、9人乗っています」
なら、式は
「4+5+9=18」。
「3台の車に6人ずつ」
なら、当然
「6+6+6=18」
と考えることになります。
しかし、この「新しい計算を考えよう」という単元に至って、ついに
「“6+6+6”のような、何かが同じ数ずつある場合は、“6×3”と書く。これをかけ算という」
ということを教わります。(つまり、“新しい計算”とは掛け算のことです)*4 *5
……という説明に、疑問を感じましたか?
東京書籍曰く、
「6+6+6」→「6×3」
なのです。
逆ではなく。
「ちなみに、3×6でもいい」
という説明もありません。

ここでは、
「1つぶんの数×いくつぶん=ぜんぶの数」
というのがかけ算の基本形である……と説明されることになります。
欄外。

6×3=18の6は「1つ分の大きさ」、3は「いくつ分」、12(原文ママ)は「全部の大きさ」を表していることが理解できるようにする。
大人向けに言うなら、
「一単位あたりどれだけであるか×何単位あるか=総数」
ということになるでしょうか。
まあ、この時点では、
「これは逆でも良くて、その場合の式は“3×6”で、前にある3が“いくつ分”で、後ろの6が“1つ分の大きさ”になるね」
……とか余計なことを言うと、学習を始めたばかりの子どもは混乱する……という配慮から、交換法則には触れないのでしょうが、その「配慮」がずっと後まで続くわけです。

「6枚のお皿に柿が3個ずつのっています。柿は全部で何個ありますか」といった問題では、十分な検討もなく、数字が出てくる順に「6×3」と書いてしまう場合がある。これは、場面を具体的に想像することなく数字だけを見て式を書いたり、乗法の式の意味の理解が十分でなかったりすることから生じると考えられる。
「いやいや、どんな理解で書いた回答でも、正解は正解だろ?」
という声が聞こえてきそうですが。
えーっと、でも、「十分な検討もなく」式を書く子、というのは非常にたくさんいます。
本校の2年生担任曰く、かけ算の学習に入る直前の子ども達に
「5こずつりんごが乗ったお皿が3まいあります。りんごはぜんぶでいくつありますか」
という問題を出したら(レディネス・テスト)、
「5+3=8 こたえ 8こ」
と書いてきた子が半数近かったそうです。
要するに、出てきた数字をとりあえず演算子でつないでるだけで、足し算がなんなのか、引き算がなんなのか、問題文で示されているのはどういった状況なのか……といったことを深く考えない子はとっても多い。
まあ、純然たる学力調査であれば、
「正解なら○。不正解は×。調査終了」
……でいいんですが、学校の「テスト」においては、不正解だった子には、なんで不正解になったのか、原因を確認し、適切な対応をしなければなりません。
だから、答えは合っていても、どうも適当に式を立ててるだけっぽい子は教師としては要注意なのですね。
……だからと言って、わかっている子にまで交換法則の使用を禁ずる理由にはならないと思いますけど。
では、東京書籍は交換法則を知らないのか、というと……。
交換法則の扱い。
東京書籍教科書では、九九は
「5の段→2の段→3の段→4の段→6の段→7の段→8の段→9の段→1の段」
の順で学習します。*6
その中頃、6の段の学習。

左下、「ゆうたさんの考え」に注目してください。
この段階で、すでに
「6×4と4×6の答えは同じだ」
といったことが子どもたちに示唆されるわけです。
のみならず、この時間では、それがかけ算一般に成り立つ規則であることを、理由付きで教わります。

●●●●
●●●●
●●●●
●●●●
●●●●
●●●●
この図の「●」の数は、
「横一列4個が6列集まっている」
と見ることも、
「縦一列6個が4列集まっている」
と見ることもできる……というわけです。
(しかし、ここにおいても「4×6」は「4+4+4+4+4+4」である、という原則はなお堅持されています)
次いで、7の段の学習。

言い忘れましたが、九九の学習では、まず自力で足し算するなどして「○の段」を完成させ、その後それを唱えて暗記する、という手順を繰り返します。
この時間は、7の段を完成させる活動です。
で、「まみさんの考え」。

ここにおいては、児童自らが積極的に交換法則を活用し、7の段を完成させることが推奨されています。
……にも関わらず、文章題において式を「逆」にすることは、九九の学習のまとめにおいてさえ認めないのです。
このような東京書籍の記述に対して、
「数学的におかしい」
「これじゃあ学力が低下するわけだ」
「日本人の思考力が(以下略)」
とか紋切り型の批判をぶつけるのは簡単ですが、これが彼らの無知によるものなのか、というと、それは教科書会社を甘く見すぎだと思います。
例えば、たぶん、私たちの多くは「にくじゅうはち」と言えば「2×9=18」を表す九九である……と信じて疑わないと思うのですが、指導書「研究編」によればこうです。

被乗数先唱と乗数先唱
乗数九九の唱え方には、被乗数先唱(被乗数→乗数→積)と乗数先唱(乗数→被乗数→積)の2つの方法がある。
被乗数先唱には、式を左から右へと書いたり読んだりすることに合致していること、aのb倍の思考の順にも適合していること、a+a=a×2の乗法の意味理解にも通じていることなどの利点がある。
また、乗数先唱には、筆算における乗法計算では乗数を基本とし、除法でも除数を基本とする習慣に合致する、といった利点がある。
このように、いずれにもそれぞれ利点があるが、現行のように被乗数先唱が用いられたのは昭和10年度(第2学年は昭和11年度)から使用した「尋常小学算術書」からである。「かける」という言葉は、数について「倍する」という意味であるとして導入する限り、九九においても、aをn倍することは「a,n」と唱えるのが自然であるといったことが被乗数先唱を採用したおもな理由であった。しかし、いつまでも被乗数先唱で通すというのではなく、一応九九を覚えるまでの過程として唱え方を一定するものであることはいうまでもない。
何言ってるんだかわからないかも知れませんが、要するに
「にくじゅうはち」は「2×9=18」と見なすという決まりはなくて、実は「9×2=18」と見なすこともできて、いずれもメリットがあるんだけど、とりあえず諸事情勘案した上で、「2×9」のことだとしておくよ?
……ということです。
しかも、
「いつまでも被乗数先唱で通すというのではなく、一応九九を覚えるまでの過程として唱え方を一定するものであることはいうまでもない」
言うまでもないらしいです。
ともあれ、このように、教科書会社は算数教育についてかなりの研究を重ねた上で教科書を作っていることはいうまでもない。
で、九九は「一応覚え」たら逆にしてもいい……のだとしたら、文章題の式を「逆」にするのはいつになったら許されるのか。
教科書の他の部分も確認してみました。
見方によっては交換できる。
「力をつけよう」の一つ前、「九九のひょうときまり」。

ひととおり九九の学習が終わった子どもたちは、このような切手シートやチョコレートの図を見せられて、
「なんとかしてこれらの総数を計算で求めるのだ。これまで習ったことをうまく使うがよい」
と要求されることになります。
左半分、切手シートについて。
ここでは、式は「8×5」と「5×8」、いずれでもよい……とされているのですが……。

それはあくまで、見方によっては
「横一列8枚が5つぶん」
と見ることも
「縦一列5枚が8つぶん」
と見ることもできるから……ということのようです。
……でもそれ、言い換えると、
「5こずつリンゴが乗った皿が3まい」
という状況をきちんと想像した上で、
(この図は教科書・指導書のものではありません)
「“一番左のリンゴ”が3個、“左から二番目のリンゴ”が3個……3こずつのグループが5組あるので、3×5」
と見なす子がいたなら、式はどっちでもいいんじゃないかと思いますけど……。
ともあれ、東京書籍的には、2年生では式の順序は固定されているなら、3年生ではどうか。
3年生での扱い。
3年生用指導書をずーっと見ていくと、「新しい算数」3の下、「かけ算の筆算(2)」において交換法則の片鱗がありました。
……ただし教師用の「注」に。
単元冒頭、

「5人がけの長いすが30こあります。ぜんぶで何人すわれますか」
一番下に、式は「5×30」である、と教師向けに明示されています。
教科書にも、
「1このいすにすわれる人数×いすの数=ぜんぶの人数」
と書いてある以上、子どもにとっても他の選択肢はありえません。
まあ、この単元は、かける数が2桁以上になる計算について学習する内容なので……。
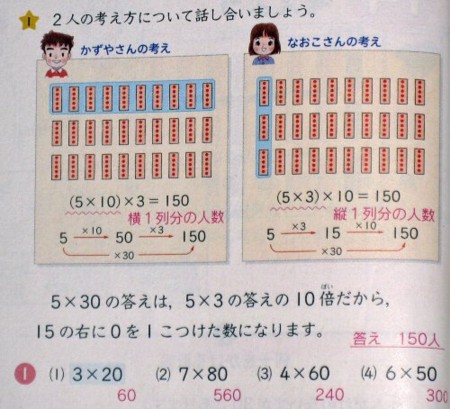
で、この式をどうやって計算したらいいか考えましょう、という中で、指導書では、子どもから「交換法則を使う」という反応が出ることが予想されています。
中央下、「ウ」をご覧ください。

「5×30=30×5=150」
ということですね。
……そういう意見が出ることは予想されているのですが、「正しい」考え方としては、
「5×30=5×3×10=15×10=150」
という手順で考えていくことになっています。
……まあ、「3×50」を交換法則で解決してしまうと、「30×50」で手詰まりになるからなんですが……。
(交換しても、「二桁×一桁」に変形できないから)
交換法則を積極的に使う場合もある……が……。
単元「かけ算の筆算(2)」の終わり近く、「かけ算のくふう」に至って、ついに「3×46」を「46×3」にして計算すると、計算が楽にできる……という事実を教科書内で扱うことになります。

しかし、例題は純粋な計算問題であって、文章題でないことに注意してください。
この「かけ算のくふう」の中でさえ、上の問題の直後
「38人にみかんを3こずつ配る」
という文章題においては、

「3×38」
が「正しい式」として示されています……。
まとめ。
……どうやら、何年生であろうと、
「5こずつのりんごが3皿」
の「正しい」式は「5×3」であって、どうしても「3×5」を使いたいなら
「5×3=3×5=15」
みたいに書かないとだめ……というのが、東京書籍ルールである模様です。
しかし、たとえ導入において「5×3」→「5が3つ(5+5+5)」と教えるにしても、これはあくまで子どもの理解を助けるための恣意的な解説……いわば漢文訓読みたいな技術であって、数学世界の決まりではありません。
現に、英語圏では「5×3」→「5 times 3」……あえて訳すなら「5回の3」……つまり「3+3+3+3+3」、と読むのだそうです。
我々大人にとっては、交換法則が正しいことは自明です。
そして、理解力のある子どもにとっても、
「3×38=38×3」
であることは、(2年生の、九九を習っている途中の段階で!)すでに自明なのです。
自明であるならば、式を立てる段階で省略しても問題ではないはず。
そんな子にまで「3×5=3が5つ」という「学校ルール」を強要する必要があるのか、という疑問が強くあるのですが……。
私なりに、まだまだ言いたいことはあるのですが、いい加減長くなったので、それはまた後日。
余談。
乗法の交換法則は、ふつう6×4=4×6のような等式と関連づけて指導するが、上記のような式は被乗数と乗数との実質的な違いを無視することによって成立する。
ところが、児童はこれまでに被乗数と乗数の使い分けについてかなり厳しく考えてきたといってよい。
それゆえ、不用意に式を導入して形式的な扱いを急ぐと、児童が混乱を起こす恐れも出てくる。
「児童は……使い分けについてかなり厳しく考えてきたといってよい」
……って、他人事みたいに。
それは自分のところで教科書をそう書いたからなんじゃ……?
*1: 「指導書」というのは、まあ教師用の資料みたいなものです。
何分冊かになっていますが、そのうち「指導書(指導編)」は、ほぼ子どもの教科書と同じ外見をしていて、授業を進める上で注意すべき注釈が入っています。
「指導書(研究編)」は、教材についての解説をまとめた本で、全ページモノクロで文章ばっかりです。
「指導編」は教室では「先生用の教科書」などとも呼ばれ、子ども時代、のぞきこもうとして拒否された経験をお持ちの方もいるのではないでしょうか。
*2: 他の会社の教科書も、地域の教育事務所に行けば置いてあると思うんですが、なにぶん平日の5時までしか開いていないので……。
さすがに休暇取ってまで見に行く気にはならなかった。
*3:そう考えると、「3×5と5×3が違うものとして教えられてる、と聞いて驚いた文科省の人」というのは、検定教科書の内容を把握してなかったことになりますね。
もっとも、2年前、まさにこの教科書を使って授業してたのに、今さら衝撃を受けている私はもっとアレなわけですが。
*4: もっとも、“ろくさんじゅうはち”のような「九九」という形で習うのはもうちょっと後ですので、式は「6×3」と書いても、実際にその答えを知るには、この時点ではまだ「6+6+6」をするしかありません。
(その煩雑さを解消するのが「九九」である……というのが、九九を覚える動機付けになるわけです)
*5: もちろん、かけ算というのは、モノを数えるだけの計算ではありません。
「時速60km×3時間=180km」
とか、
「底辺×高さ=面積」
とかいう場合もあります。
しかし、そういう直接数えられない値を計算対象にするのは、多くの2年生にはまだ荷が重いので、この段階では「ひとつ、ふたつ……」と数えられるようなものを扱うことになります。
(「7の段」の学習にいたって、ようやく「7cmのリボンがn本」を扱います)
*6: 従って、件の「5×3」と書いて不正解になった子は、5の段も3の段もすでに両方習ってるんじゃないかな、と思います。
